Reverse Triangle Inequality
The reverse triangle inequality, sometimes called the circle inequality (see below) is a simple consequence of the triangle inequality.
For any \(\boldsymbol{x}, \boldsymbol{y}\) in a normed vector space \((X, \|\cdot\|)\)
Proof
We first consider the norm of \(\boldsymbol{x}\) expressed in terms of \(\boldsymbol{y}\), and apply the triangle inequality:
This implies that:
Since \(\boldsymbol{x}\) and \(\boldsymbol{y}\) are generic, we also have that:
Combining these results we have the desired inequality:
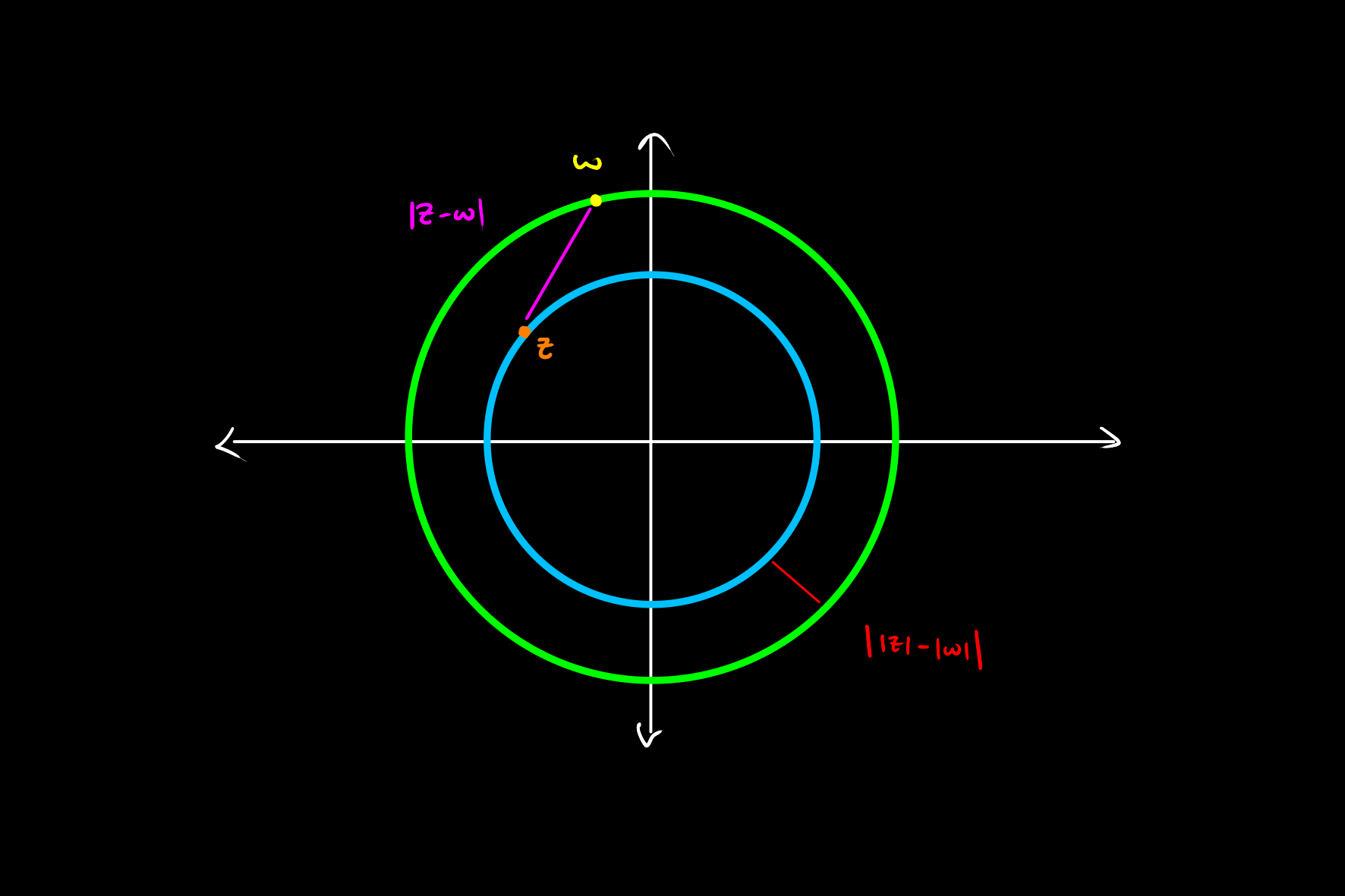
Geometric Intuition
This inequality is also sometimes called the circle inequality due to the below interpretation in \(\mathbb{R}^{2}\) with the Euclidean norm or \(\mathbb{C}\) with the complex modulus.
Given two complex numbers \(z\) and \(w\), with two circles drawn for the set of points with modulus equal to that of \(z\) and \(w\) each. Then, \(|z - w|\) is the distance between a point on the inner circle and a point on the outer circle, while \(||z| - |w||\) is the difference between the radii of the two circles. The latter is the minimum of the former.
